|
|
| ミランコヴィッチメニューへ戻る 一般大気循環理論 224p ロシア語 モホフ、A.V。エリセエフ、K.M.。 シャンタリンスキー https://core.ac.uk/download/pdf/197368962.pdf 第1章 第2章 第3章 第4章 第5章 第6章 第7章 参考 4章 一般的な大気循環の流体力学モデル 4.1 温度と風速の帯状分布のモデル化 4.2 大気の一般循環のスペクトル流体力学的モデル 4.3 ロシアの水文気象センターのグローバルスペクトルモデル 4.4 大気修正セミラグランジュの季節大気循環モデルの再生 4.1 気温と風速の帯状分布のモデル化 帯状モデルでは、垂直方向の動きがない場合、緯度の円に沿って動きが発生すると想定されています。この場合、熱流方程式は大幅に簡略化され、運動方程式とは別に解くことができるため、温度場と風速場を互いに独立して計算することができます。 気温と風速の帯状分布をモデル化する問題は、S.A。によって解決されました。マシュコビッチ。彼の基本的なモノグラフ(Mashkovich、1986)で、彼は定式化、問題を解決するための方法、および行われた作業の主な結果について概説しました。帯状循環を記述するための次の連立方程式が、初期の連立方程式として採用されました。ES 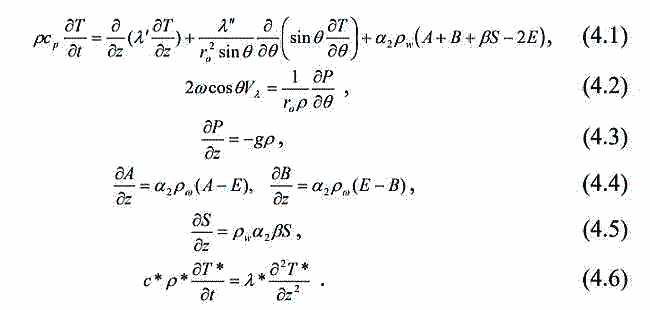 以下再調整 ここで、zは海抜の高さ、ρは空気密度、ρwは水蒸気の密度、Aは上から下に向けられた長波放射の流れ、Bは下から向けられた長波放射の流れです。上に、Sは短波(太陽放射)の流れ、4TfE-大気放射、f-ハルバートによる選択的吸収を導入する通常の割合、σ-シュテファン-ボルツマン定数、-乱熱伝導率垂直方向に沿って、-水平方向に沿った乱流熱伝導率、*-下にある100の媒体(土壌または海)の熱伝導率、*およびC *は、下にある密度と比熱容量です。それぞれ、Cpは一定圧力での空気の比熱容量、T *は下にある媒体の温度、и1と2はそれぞれ短波と長波放射の水蒸気の吸収係数、21 /、Гは、下にある表面の特性、曇りなどに応じた総アルベド、tW)、(は太陽エネルギーでは、単位表面あたりの単位時間あたりに来る、K *-下にある媒体の熱拡散係数。システム(4.1)-(4.6)は、垂直座標zに8次があり、zに8つの境界条件を設定する必要があります。以下が作品に受け入れられました。 1.大気の上限に外部からの長波放射のフラックスがない:zでА0。 (4.7)2。雲、地球の表面などからの部分反射を考慮に入れた、太陽から来るエネルギー。惑星間空間への侵入は、大気の上限で次のように書かれます:SГtWtwt)、()、()、(1atz。大気の上部境界での流れは、垂直方向に沿って熱します。これは、垂直方向の温度勾配がゼロに相当します。Тz0/z。(4.9)4。海面(z = 0)で、条件下にある表面の熱バランスが満たされている: 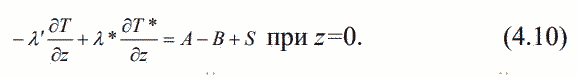 5. z = 0では、下から上に向けられた長波放射のフラックスは、下にある固有の放射と等しくなければなりません。表面: qf係数は、下にある表面からの放射が黒体からの放射に近いことを示しています。  6.下にある媒体と隣接する空気層の温度は同じです。  7.基礎となる環境のある深さで、温度は一定になります。  8.大気の上限では、対数微分圧力からゼロに等しい:  S.A. Mashkovichは、気象量の任意の初期分布と、太陽からの熱流入の変化について、連立方程式の解を探しています。 必要な関数または指定された関数fは、次の2つの要素の合計として表されます。  ダッシュの付いた文字は、気象値の定常的な年間平均分布に対応します。ただし、wは、入射する太陽エネルギーの年間平均値を示します。この問題における気温と風の平均年間分布は既知であると考えられます。関係(4.15)は、方程式(4.1)-(4.6)と遊び条件(4.7)-(4.14)に代入され、連立方程式を得ることができます。年間平均値からの気温と放射フラックスの偏差。このシステムは、時間のw変動の任意の特性と任意の温度分布に対して解かれます。 次に、元の方程式が変換されます。 領域z0では、z座標の代わりに、新しい独立変数が導入されます-層の光学的厚さx: 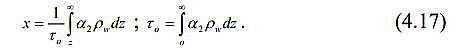 次に、輻射と気温Tを結ぶ式を使用して、気温を初期方程式から除外します。 このために、温度は式(4.15)に従って放射4TfEの式に代入され、得られた式は線形化されます。 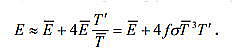 そこからそれは続く  ここで、EとTは平均年次値からの偏差です。 式(4.18)および(4.17)を使用すると、元の連立方程式は次の形式になります。 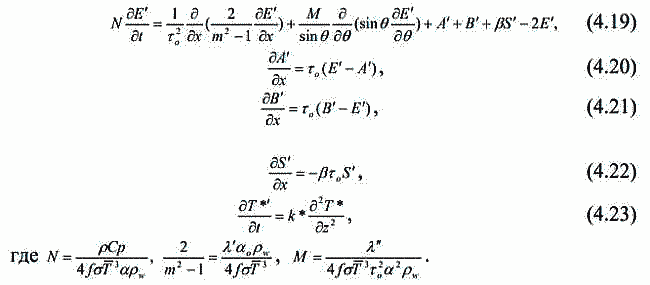 変換された境界条件は次のように記述されます。 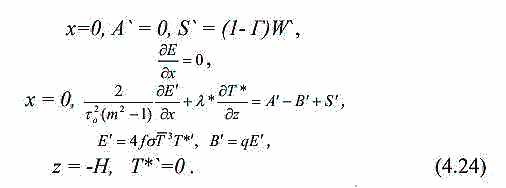 値N、m、Mは一定であり、m 2 = 3であり、方程式の文字の素数は以下では省略されています。 S 'の境界条件を考慮した方程式(4.22)の解は、次の形式で記述されます。 関数W(θ、t)は、通常のルジャンドル多項式Pn(θ)の級数として表され、係数は 時間:  初期温度場(4.16)も同様に表されます ルジャンドル多項式のシリーズ 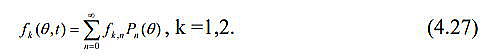 方程式(4.19)-(4.21)、(4.23)の解も、xとtに依存する係数を持つ通常のルジャンドル多項式の級数の形で求められます。 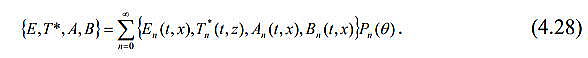 級数(4.28)は、等式nPyPnnを使用し、同じインデックスを持つルジャンドル多項式で項を収集して、方程式(4.19)-(4.23)に代入され、求められる展開係数の連立方程式を取得します。 S.A. Mashkovich(1958)は、分析形式で問題の解決策を取得しました。得られた解は、大気の所与の初期状態および時間経過の任意の特性について、任意の瞬間の大気中の空気およびその下にある媒体の温度、放射および長波放射のフラックスを計算することを可能にした。太陽からの熱流入の。帯状風速の計算式は次のように導き出されます。まず、静的方程式がクラペイロン方程式を考慮して統合されます。これにより、よく知られている気圧式が導き出されます。  式(4.29)は対数化され、次に微分されます θを超えると、 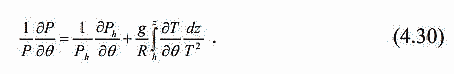 hの場合、境界条件(4.14)を考慮すると、式(4.30) 次の形式になります。  状態方程式RTpを考慮に入れると、等式(4.31)は次の形式で記述できます。  式(4.2)に(4.32)を代入した後、温度場から帯状風速を決定するための最終式が得られます。 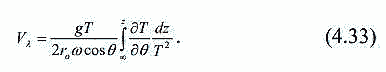 得られた解は、異なる高度での帯状循環と帯状温度の年次変動を理論的に構築し、大気の初期状態の影響の減衰のプロセスと対応する体制の確立を研究するために、研究の著者によって使用されました与えられた熱の流入に。帯状温度と風速の年間変動を構築するために、関数W(θ、t)の値が指定されました。これは、太陽からの年間熱流入を表します。 計算結果は表と図で示されています。だから、図では。 4.1は、海面での帯状温度の子午線分布を示しています。北半球で理論的に得られた地温の年間変動は、実際の変動に近いことがわかります。年間の気温変化の振幅は正しく決定されており、特に振幅が大きい高緯度で良好な結果が得られました。計算された温度と実際の温度の間の不一致は3°Cを超えません。最大の誤差は低緯度を示します。南半球の場合、計算結果はあまり成功せず、誤差は10°Cに達しました。 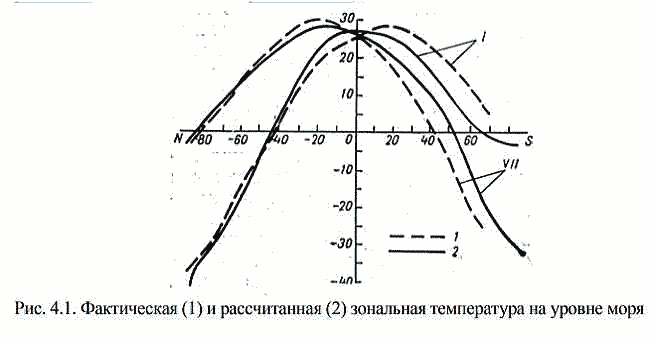 図: 4.1。 実際の(1)および計算された(2)ゾーンの海面温度 この研究(Mashkovich、1986)は、地球の近くと高さ(最大12 km)の両方で、1年のさまざまな月の気温と風速のゾーン値を計算した結果を示しています。結論として、1月と7月の北半球の対流圏と下部成層圏における計算された実際の帯状風速の分布を考えてみましょう(図4.2)。この図は、ジェット気流の明確なコースがあることを示しています。 1月の最大風速域は、北緯40度付近です。高度12kmでの最高速度値は38m / sに達します。 7月に、この地域は北に移動し、北緯50度に位置します。ジェット気流の速度は大幅に低下し、高度12kmでの最高速度は24m / sです。北緯25度以南。東風のある地域が現れ、その速度は12 km 13 m / sに達します。一般に、実際の値と計算された値の間には良好な一致があります。 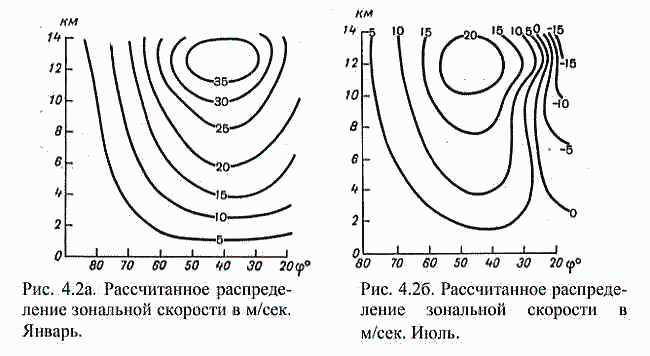 図: 4.2a。 計算された帯状速度分布(m / s)。 1月。 図: 4.2b。 計算された帯状速度分布(m / s)。 7月。 4.2。 大気の一般循環のスペクトル 流体力学モデル作業に続いて、ロシア水文気象センター(SMA)の大気の一般循環のスペクトルモデルを考えてみましょう(Degtyarev、2008年)。 このモデルは、準静的近似における水熱力学の連立方程式の数値積分に基づいています。 連立方程式は、運動方程式で構成されています 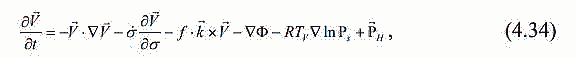 熱流方程式 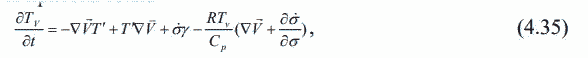 水分移動方程式 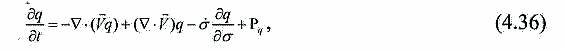 表面圧力トレンド方程式  静水圧方程式  さらに、診断関係は、р-uσ座標系および次の垂直速度のアナログに使用されます。 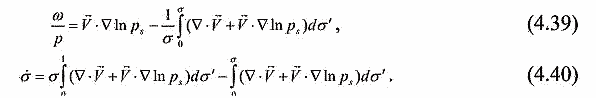 ここで、TVは仮想温度、Tは特定の標準プロファイルT®()からの温度偏差です(モデルの現在のバージョンでは、To = 300 K)。 p-圧力; psは表面圧力です。 V-水平風速のベクトル。 fはコリオリパラメータです。 /TCRTVpV/-静的安定性パラメーター。 k-垂直ベクトル、-ジオポテンシャル; -水平勾配演算子。 A-ベクトル場Aの水平発散; -積分の変数。式(4.34)と(4.40)はσ座標系で記述されています。式(4.34)-(4.38)の右辺は、断熱過程とサブグリッドスケールのダイナミクスによる気象量の変化への寄与を表しています。大規模な数値天気予報と大気循環のモデリングに不可欠な物理プロセスの説明は、パラメータ化を使用して実装されます。予測気象値による局所的な物理的プロセスの影響の決定。運動方程式(4.34)は、相対渦の垂直成分кと風速の発散、Dの方程式に変換され、の極に特異点はありません。球の表面:107 ln [)(] s PHVpTRkVft 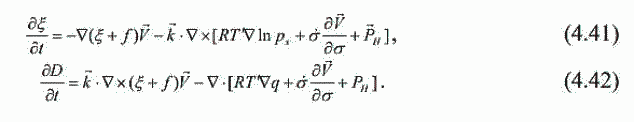 垂直導関数を近似するために、有限差分法が使用されました。 雰囲気は垂直に15のレベルに分かれています。 主な予測変数と診断変数は、レイヤーの中央で計算されます。 層の境界で、σ座標系の垂直速度と放射フラックスのアナログの値が計算されます。 モデルの主な垂直レベルでのσ値は次のとおりです:  この問題は、地球の表面()1(および上位レベル()0(。上限と下限で運動条件が設定されている)で囲まれた大気層の球または半球で解決されます。 0と1、および0では、熱、水分、運動量のフラックスがないための条件が設定されています。地球の表面の境界条件として、いくつかの特性が設定されています。 連立方程式は次のように解かれます。三角トランケーションを使用したスペクトル法。計算は、ガウス(緯度が不均一)グリッドで約2.5ºの空間解像度に対応するT40バージョンを使用して実行されます。半陰的Nemchinov-Sazonov-Robertスキームは時間積分スキームとして使用されます。モデルでは、数値モデルに明示的に含めることができない小規模の物理的大気プロセスのパラメータ化に多くの注意が払われています。 これらには、乱流および対流運動、水、雲の相変態が含まれます。大気中の太陽放射フラックス。大規模なOVA電流は、パラメトリックにのみ考慮に入れることができます。小規模な物理プロセスの記述は、モデルパラメータ(いくつかの仮説と経験的関係を使用した大規模な変数)を使用して実行されます。流体力学モデルで使用されるパラメータ化スキームは、計算効率の観点から許容できるものである必要があり、計算されるすべての物理コンポーネントの精度はほぼ同じである必要があります。ロシア連邦の水文気象センターのCMAで、次のパラメータ化スキームが開発されました。 4次の線形水平拡散、表層とその上での垂直拡散流、大規模な凝縮、湿った対流、表面でのプロセス土壌では、太陽放射と曇り、地形性重力波。 SMAの助けを借りて、この作業(Degtyarev、2008)は、主要な計測量の月平均フィールドを再現しました。モデルがOACの主要なプロセスを適切に再現していることが示されています。モデルをテストするために、20年間の気候数値実験が実施されました。実験では、自然な日射のコースが設定されました。 SSTの値、下にある表面のアルベド、および周極領域の海氷の端の位置は、月平均の気候値で表され、月ごとに変化します。 すべての気象値は、統合の2年から20年の平均によって得られました。実験の結果は、気候値、NCEP / NCAR再分析データ、および同様の研究からのデータと比較されました。数値実験の結果を順番に考えてみましょう。圧力場は海面で再現されました。図では4。3、1月の特徴であるアイスランドとアリューシャンの最小値とシベリアのアンチサイクロンの領域がはっきりと見えます。これらのCDAの位置は、再分析データによると、気候CDAの位置とかなりよく一致しています。 北半球(SP)と南半球(SP)の気候亜熱帯高気圧の位置もうまく再現されており、これはモンスーン循環のモデル化にとって特に重要です。モデル計算ではRMSD値が過小評価されていますが、1月の圧力の最大RMSD値の位置は確実に再現されています。 7月のSP循環は、サイクロン活動が顕著であるSPよりもスムーズです。 7月の海面における圧力の主な極値の地理的位置(図4.4)は、再分析の気候データに対応しています。 7月のRMS値は、温帯緯度で最も高く、特にSPのアイスランドとアリューシャンの最小値とSPの低圧帯で最も高く、これらの緯度でのサイクロンの生成と移動に関連しています。当然のことながら、この時期の大気プロセスは大幅に悪化するため、圧力のrms偏差は各半球の冬の値が高くなります。 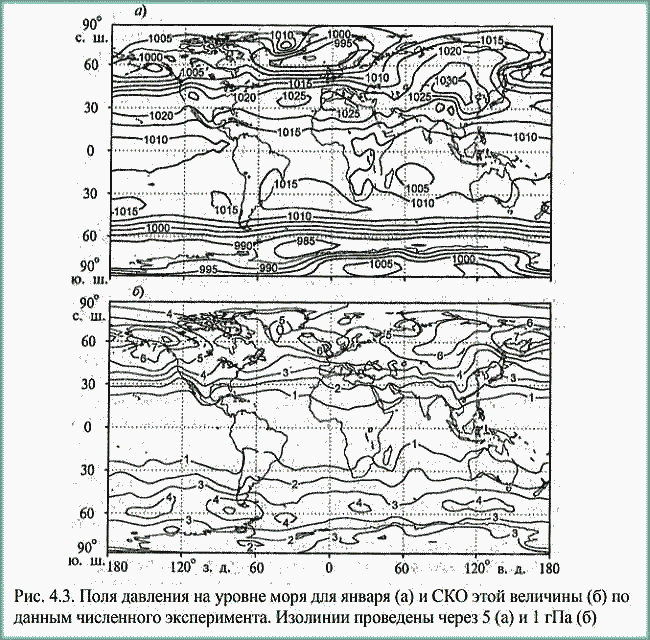 図: 4.3。 数値実験のデータによる1月の海面での圧力場(a)とこの値のRMS偏差(b)。 等値線は、5(a)および1 hPa(b)の後に描画されます。 850 hPaの等圧面でのモデル気候の風レジームは、気候データに対応します。AT850の赤道付近で、半球の中緯度と向流の両方で西向きの海流が優勢です。 1月には、合弁事業の西部の流れは7月よりもはるかに強くなります。偏西風は太平洋上で最大値に達しますが、再分析の気候データに対応する大西洋上ではそれほどではありません。 それどころか、7月には西側のSPへの流入が激化する。 SMAは、熱帯地域の風の状況の季節変化を確実に再現します。モンスーンの循環は、インド地域、東南アジアおよび他のモンスーン地域で明らかになりました。 7月のAT850マップは、SPのインド洋上の夏のモンスーン循環によって東貿易風が「中断」されていることを明確に示しています。 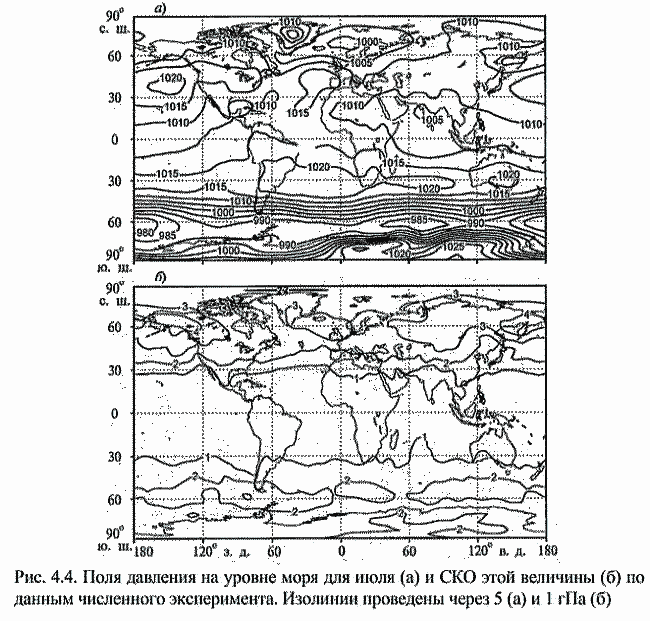 図: 4.4。 7月の海面での圧力場(a)とこの値のRMS(b) 数値実験からのデータ。 等値線は、5(a)および1 hPa(b)の後に描画されます。 AT200の等圧面では、上部対流圏の北半球と南半球の亜熱帯海流がはっきりと見えます。それらの強度は、各半球の冬期に最大になります。熱帯地域では、インド地域のモンスーン循環の主な特徴がうまくモデル化されています(まず第一に、これはチベット上の高高度高気圧です)。 1月と7月の帯状風速の高度-緯度図も作成されました。 実験データは、上部対流圏の北半球と南半球のジェット気流の111の緯度と高度の位置が非常にうまくモデル化されていることを示しています。ジェット軸の最大風速値は、各半球の冬に到達し、季節ごとにスムーズに変化します。冬の成層圏では、西風速が1 hPaの表面まで上昇し、ジェット軸が北にシフトし、緯度が約60度になります(図4.5)。 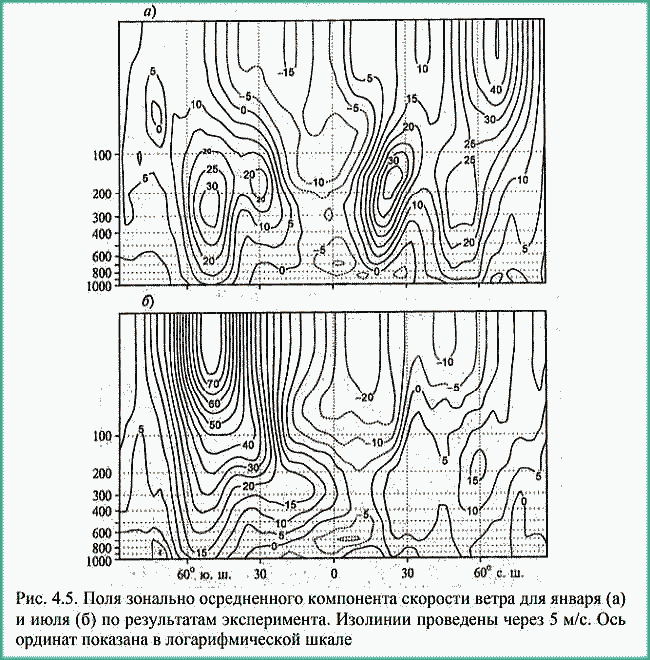 図: 4.5。 実験結果による1月(a)と7月(b)の帯状平均風速成分の場。 等値線は5m / s間隔で描画されます。 縦軸は対数目盛で表示されます。 モデル大気の熱レジーム実験結果による1月と7月のゾーン平均平均気温の高度-緯度図を図1に示します。 4.6。 赤道対流圏界面の領域の最低気温は約190Kに相当します。 これは、ほとんどすべての数値モデルに固有の気候データよりもやや寒いです。 再現された極小値は、気候データと一致しています。 下部対流圏の気温変動の年間経過はよく表現されています。 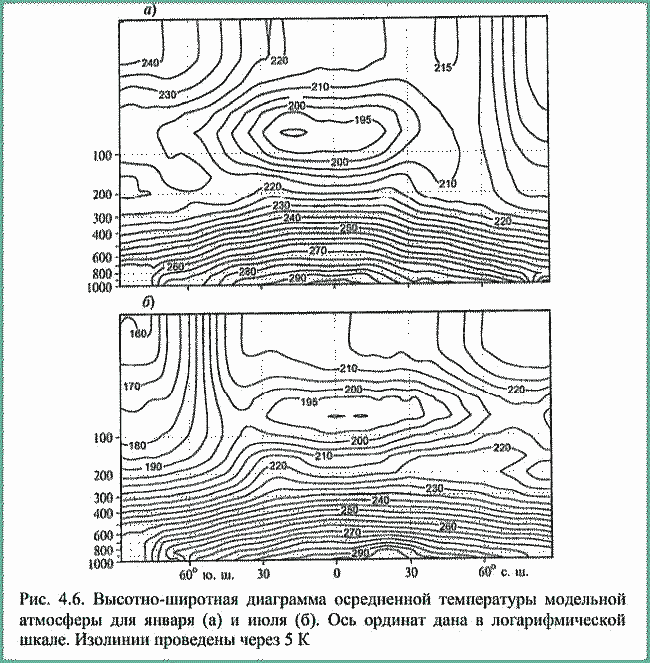 図: 4.6。 1月(a)と7月(b)のモデル大気の平均気温の高度-緯度図。 縦軸は対数目盛です。 等高線は5K後に描画されます 下にある表面のレベルでは、最低温度はシベリアの最高気温、カナダ北部、グリーンランドで観察されます。 SPの1月の地表面のゼロ等温線は、イングランドから中央ヨーロッパを経由してアゾフ海の海岸、さらに南(北緯32度、東経60度まで)を通過し、その後太平洋に到達します。朝鮮半島の北。 1月のSPでは、すべての土地(南極大陸を除く)が正の気温の地域にあります。 7月に、下にある表面の最高気温の値は、サハラで308Kに達し、北アメリカの南、南アメリカの北、インド、インドネシアで300Kを超えます。 これは、気候データに対応します。陸上での1月の最高のRMS値は、北米の東部と南西部、中央ヨーロッパとオーストラリアで観察されました。 7月には、RMSが小さくなります。表面温度のRMSDの最大値は、南アメリカの南部、中国の東、北アメリカの北西にあります。 RMS温度の値の増加は、この地域でのサイクロンの通過、および海と陸の海岸線の特徴に関連しています(図4.7、4.8)。モデルは、輻射と熱のバランスを計算します。大気中の放射フラックスは、極と赤道の間の温度勾配を設定および維持します。 これにより、大気中に傾圧波が発生する条件が作成され、大規模な大気プロセスの発達が大きく左右されます。表面からの顕熱HFLおよび潜在QFL熱の乱流フラックス、大気の下部(上部)境界での長波長FLB(FLT)および短波長FSB(FST)放射のフラックス、放射の平均年間値大気のRBBの下部とRTBの上部の境界でのバランス、およびTBS表面上の総熱バランス。計算結果を表4.1に示します。数値実験によると、顕熱と潜熱の乱流フラックスは大気循環の保守的な特性です。放射特性の値は、気候の値とよく一致しています。 SPの表面の熱収支は、1月に負、7月に正になります。 SPでは反対の画像が観察されます。 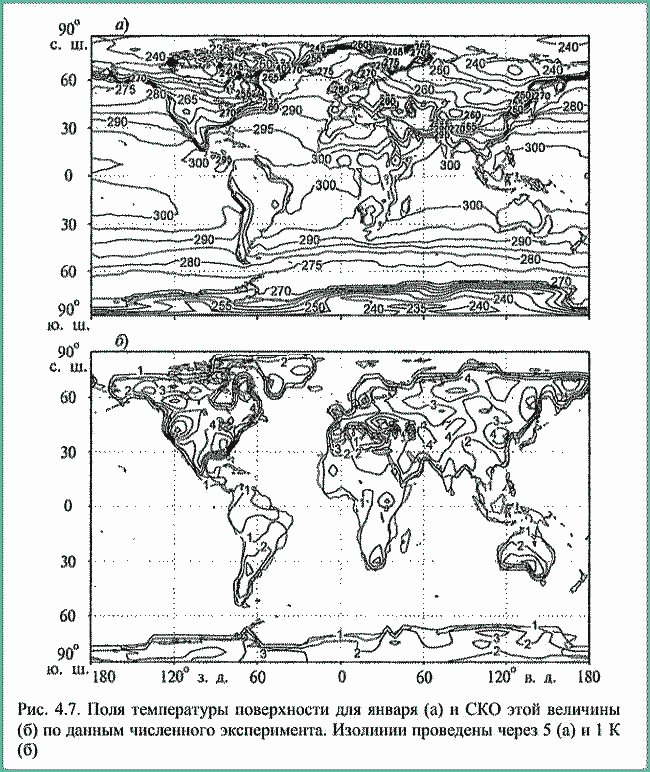 図: 4.7。 1月の表面温度場(a)とこの値のRMS偏差 (b)数値実験のデータによる。 等値線は5(a)と1Kを介して描画されます (b) 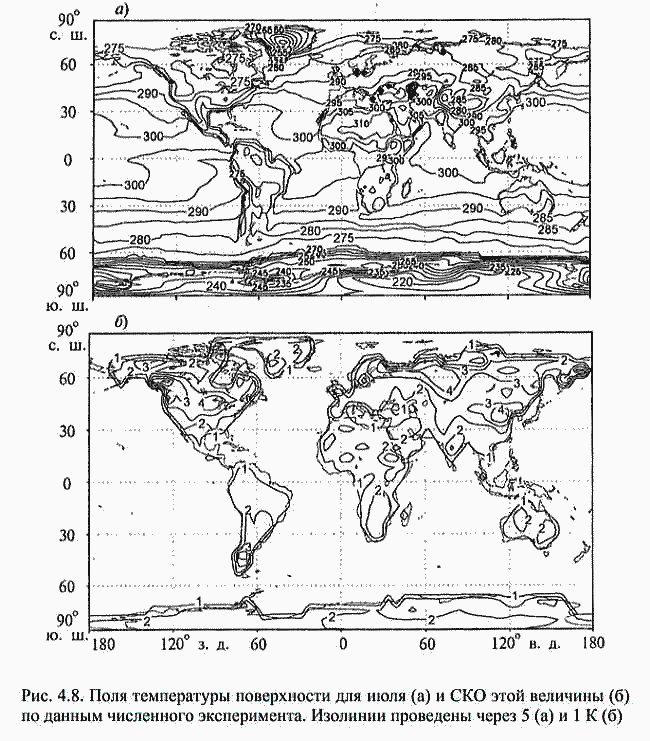 図: 4.8。 7月の表面温度場(a)とこの値のRMS(b) 数値実験によると。 等高線は5(a)と1 K(b)を介して描画されます 1月と7月の水分の質量分率の帯状平均分布が得られました。計算によると、水分の質量分率の最大値の領域は、WZKの緯度方向の動きに従います。 1月には、赤道近くとSPの熱帯緯度に位置します。 7月にIBCがSPにあるとき、水分の質量分率の最大値の領域も北にシフトします。水分の質量分率の極大値は、116の緯度の中央にあります。この場合、冬のSPの下部対流圏の水分の質量分率の最大値は夏の約2分の1です(図4.9)。 表4. 11月と7月のモデルによる統合20年目の輻射熱収支(W / m2)とその構成要素 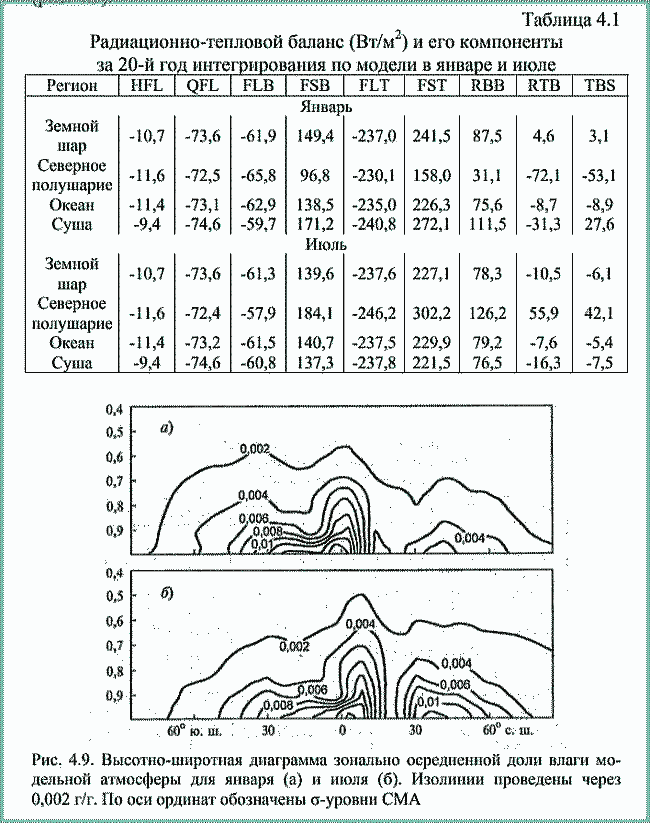 図: 4.9。 1月(a)と7月(b)のモデル大気の帯状平均水分率の高度-緯度図。 等値線は0.002g / gで描画されます。 縦軸はSMAのσレベルを示しています 1月の降水強度が最も高いのは、SPの熱帯緯度であり、冬季のWZKの位置によって決まります。 7月には、モンスーン循環の影響で、インド亜大陸と東南アジア地域に大雨が降ります。過渡期には、赤道域で最大の降水強度が観測されます。 最大降水量の地理的領域は、気候の状況を非常によく反映しており、IBCの移動の季節的な経過を繰り返します。中緯度では、降水強度が増加した地域は嵐の軌跡と一致します。中緯度低気圧の主な動きの軌跡で。 SPの中緯度での最大降水量は、強度と地理的位置の観点からうまくモデル化されました。 SPでは、それはやや過小評価されています。 7月の赤道では、最大降水強度が過小評価されています(4 mm /日)。フィールドデータによると、6 mm /日です。中緯度での降水強度の最大値は、SPとSPの両方で正常にモデル化されています。移行期間中(4月、10月)、最大降水量は赤道地帯でも発生します。降水強度のRMSDの最大値は、気候値に近いです(7月には、インド地域と東南アジアで4 mm /日に達します)。熱帯では、モデル降水量は対流特性を持っており、これは現実に対応しています。モデル実験での大規模な結露による降水量は、主に中緯度に降ります。 検討対象のモデルA.I.の作成者Degtyarevは、OCAの要素をシミュレートするために、いくつかの成功した数値実験を実行しました。1987年10月の東ヨーロッパでのブロッキング状況を再現するため。大西洋の海面水温の異常が大気循環の発達に及ぼす影響。冬季と夏季のモンスーン循環の平均特性のモデル化には特に注意が払われています。 SMAは、インドの夏季モンスーンのフェーズ、上部対流圏でのチベット高気圧の移動、主なジェット流とモンスーン海流の局在と強度(上部対流圏での西部と東部の亜熱帯、および下部対流圏)。 7月のインドにおけるモデル降水量の最大値は21mm /日でした(再分析データによると-22mm /日)。 SMAは、南アジアと東南アジアのモンスーン循環の年々変動をうまく再現しています。長期数値実験(モデル時間の20年間)の結果は、SMAがACの年間サイクルを適切に再現することを示しました。大気の月平均気候特性-基礎となる表面システム、すなわち:ACダイナミクス、その熱および放射レジーム、および水循環は、正常に再現されており、このクラスの他のモデルの結果に対応または上回っています。 4.3 ロシア水文気象センターのグローバルスペクトルモデル ロシア連邦の水文気象センターの大気の基本的なスペクトルモデルは、運動方程式、静水圧、連続性、熱を含む、バロクリニック大気の水文熱力学の方程式のシステムに基づいています。風速の垂直成分の流入、水分移動、および診断関係。方程式の右辺に含まれる熱と水分の発生源を決定するために、サブグリッドプロセスの一連の物理パラメータ化が使用されます:放射伝達、対流、乱流、沈降、下にある表面のプロセス(Rozinkina et al。、 2010)。スペクトル表現の便宜のために、速度の運動方程式は、渦と発散の方程式に変換されます。 垂直領域10はN層に分割され、N-1レベルで区切られ、σの値が固定されています(σ= P / Ps、ここでPsは地表の大気圧、pは圧力です) σレベルで)。モデルの主な変数(温度、風速の水平成分、混合比)がレイヤーに対して定義されているため、計算された値は、半整数σで識別される中間σºの値に割り当てられます。 インデックス。シグマ座標を使用すると、モデル内の地形の影響を考慮に入れて、下限条件の定式化に関連する問題を回避できます。 119 OCAモデルの方程式の解が求められる領域は、下にある表面(陸または海)と、計算レベルの上限σº-半整数インデックスσ(1/2)の値を持つ上限によって制限されます。 )(大気モデルの上位計算レベル)。大気モデルの既存の運用バージョンでは、σº= 0.1であり、σ= 0およびσ= 1で垂直速度がゼロであるという条件を考慮すると、水域では約10hPaに相当します。 各タイムステップで計算される求められる変数は、速度ベクトルの水平成分、発散、風速の渦、気温、湿った空気の混合比、表面圧力、下にある表面の温度、上層土層、および積雪の厚さ。さらに、各時間ステップで、降水量(対流および大規模)の合計、基礎となる表面熱収支の成分、基礎となる表面放射収支の成分、表面摩擦応力、および放射熱が大気に流入します。計算されます。独立変数:球座標系の時間tと座標(λ、φ、σ)。方程式を解くために、次の境界条件が使用されます。 -垂直速度の場合、垂直速度のゼロに等しい条件がσ= 0およびσ= 1に設定されます。 -予測変数の場合-温度、湿度、風速の成分-上限カウントレベルを超える「サブグリッド物理学」の要因の作用によって引き起こされる流れの欠如。統合領域の下限は、水域上の海面として、および陸域上のアクティブな土壌層間の境界として定義されます。 同時に、大気と海洋の境界については、下にある表面の放射バランスの成分と水に近い層の乱流運動によるフラックスの制限はありません。大気と陸の境界面の場合、活性層の温度と湿度の方程式が解かれます。その結果、各時間ステップについて、土地のアクティブな表層の温度TSと湿度WSの新しい値が計算され、次の熱と長波放射バランスの成分の値が変調されます120タイムステップ。 この場合、活性層から内側の土壌層への流れの大きさは、特定のセルの温度と水分含有量の一定値を設定することによって決定されます。初期条件は、時間微分を含まない連続の方程式から求められるため、垂直速度には必要ありません。 「スペクトルモデル」技術のメインモジュールに加えて、2つの必須モジュールがあります。前処理と後処理です。主なタスクは、計算グリッド上の大気モデルのスターターキットを準備することです(前処理)。 、したがって、通常の緯度グリッドと等圧垂直システム上のユーザー向けの情報。座標、および-いくつかの診断特性の計算。 (Rozinkina et al。、2010)では、大気モデルの方程式を解く方法が説明されています。モデル方程式を統合するためにスペクトルグリッド法が使用されています。モデルの構造には、いくつかのブロックが含まれています。 通常モードの初期化ブロックです。グリッド空間での計算のブロック。 「サブグリッド」プロセスのパラメータ化のセットのブロック。リストされている最後のブロックには、次のサブブロックが含まれています。対流;垂直拡散、大規模な凝縮、下にある表面での計算のサブブロック。モデルのタイムステップでの計算の2番目の部分は、スペクトル係数の空間で実行されます。 ov(スペクトル空間での計算のブロック)。その後、グリッド空間への遷移が実行されます。この作業では、ソフトウェアパッケージの構造と、「前処理」および「後処理」のコンポーネントを含む、機能するテクノロジの一般的なスキームについて説明します。ロシア水文気象センターの全球予報モデルの主な計算技術は次のとおりです。-観測データを同化するためのシステム。 -統計的通訳システム; -海洋の活性層の診断と予測のためのシステム。 -風波の数値予測; 121-diシステム-複雑な診断指標(傾圧指標、正面パラメーター)を使用した診断および検証システム。 -航空予報の情報を計算するためのシステム(対流圏界面の高さ、対流層の特性、ジェット気流の特性); -アンサンブル予測のシステム。全球大気モデルの主な目的は、地球全体の流体力学的予測を作成することです。短期および中期のグローバルアンサンブル予測システムの開発に特に注意が払われています。アンサンブルは、わずかに異なる初期データから始まる予測のコレクションです。対応する初期データのアンサンブルは、育種法を使用して生成されます。 この方法は、最速成長モード成長方法と呼ばれ、最も単純で、必要なコンピューターリソースが最小です。アンサンブルは、妨害されたデータに基づく5組の予測と1つの制御予測(摂動されていない初期データに基づく予測)を含む11のメンバーで構成されます。 2007年から2009年の期間。ロシアの水文気象センターでは、中程度の緯度でそれぞれ約60kmと35kmの空間分解能を持つ大気T169L31とT339L31のスペクトルモデルの新しいバージョンの開発に積極的な作業が行われました。新しいバージョンの大気モデル(T169 L31)は、大気中および地球の気象要素の予測の両方で、T85L31バージョンと比較して推定レベルを超えていることを示しました。 4.4 修正されたセミラグランジュ大気モデルによる季節大気循環のシミュレーション 一般大気循環(GLAV)のセミラグランジュグローバル有限差分モデルは、INMRASとロシア水文気象センターで作成されました。移流を表すセミラグランジュ法により、クーラント条件によって決定されるステップよりも数倍大きいモデルで時間ステップを使用することができます。このモデルの大気ダイナミクス方程式を解くためのブロックの特性は、非移流レベル項を近似するための不偏グリッドでの4次有限差分の使用と、予測変数としての絶対渦と発散の垂直成分の使用です。 このモデルには、Meteoによって開発された、サブグリッドスケールプロセスの一連のパラメーター化(短波および長波放射、深浅対流、プラネタリー境界層、重力波の減速、下層表面との熱および水分交換のパラメーター化)が含まれています。 -フランスのグローバル運用モデルARPEGEおよび国際コンソーシアムALADINの地域モデルのフランス。パラメータ化の説明は、モデルの作成者の作業に含まれています(Tolstykh、2010)。経度0.9度、緯度0.72度の解像度を持つ大気のセミラグランジアンモデルのバージョンは、運用テストに合格し、ロシア水文気象センターで実装されています。 このモデルは、陸面のプロセスのパラメータ化のさまざまなバージョンを使用して、季節的な時間スケールの大気循環を再現するために使用されました。 2005年から2006年。大気のセミラグランジアンモデルの以前のバージョンを使用した最初の一連の数値実験は、ロシアの水文気象センターで実施されました。 2 NCEP | NCAR再分析が初期データとして使用されました。海面水温(SST)フィールドは、海面水温変化の単純なスキームを使用して設定されました。SST異常の保存方法が使用されました。モデルの海氷は、表面温度が–1.820 C未満の海域として定義されます。モデルの大気の解像度は、経度1.40625度、緯度1.125度、垂直方向に28シグマレベルでした。 時間ステップは36分でした。その結果、モデル全体として、中緯度の対流圏のジオポテンシャル、気温、風をうまく再現できることがわかりました。同時に、次の欠点が確認されました:熱帯における非現実的な降水量、赤道南アメリカにおけるそれらのほぼ完全な欠如。表面の高さが500hPaの場合の熱帯の平均誤差は40mで、温度が850hPaの場合-1.8度でした。南極大陸では、850hPaのレベルでの平均気温誤差は+8度に達しました。このバージョンのモデルでは、植生の存在も土壌の特性も考慮せずに、地表面のプロセスの単純なパラメーター化が使用されました。 大気の平均季節循環を現実的に再現するために、モデル時間の毎日、深層土壌層の温度と含水量の完全な緩和が、平均気候(年変動を考慮)値に実行されました。再分析データから–2。熱帯における大気循環の再現の誤差は、主に、潜熱フラックスに大きな影響を与える植生を記述するためのモデルの古いバージョンがないことに起因すると考えられています。 モデルの新しいバージョンでは、地表面のプロセスの古いパラメータ化が、植生が侵入した降水を遮断して蒸発させる能力と熱慣性を考慮した、より新しいもの(ISBA)に置き換えられています。植生の。モデルには、土壌の凍結と解凍に関連するパラメーター化が含まれていました。 ISBAのパラメーター化には、表面の物理的および地理的特性(砂と粘土の割合、土壌と植生の活性層の深さ、土壌と植生のアルベド、葉面積、表面抵抗)に関する情報が必要です。モデル計算では、深層土壌層の含水量の初期データとして、再解析データ-2などに基づいてスケーリングされた土壌含水量を使用します。表面パラメータ化の変化に対する平均季節モデル大気循環の応答を調査しました。 。 2007年10月23日から7月23日までの季節予報のアンサンブル技術を使用して数値実験を実施しました。摂動初期データのアンサンブルを生成するために、速効性摂動を成長させる手順を使用しました。 すべての計算は、モデル時間の4か月間実行され、過去3か月間処理されました。結果は、ISBAパラメータ化を使用したモデルのバージョンは、ゾーン平均降水量を大幅に再現する一方で、熱帯における降水量の地理的分布がより現実的になることを示しました-有意な降水量は南アメリカの赤道に現れ、南部の降水量の分布アフリカの半分は観測に近づきました。これは、植物が水分を保持して蒸発する能力を考慮に入れた植生のパラメータ化を含めると、からの蒸発が急激に増加するという事実によって説明されます。 地表。同時に、850hPaのレベルでの温度場の誤差の顕著な減少も認められました。次に、モデル内のサブグリッドスケールプロセスのパラメーター化のさらなる近代化が実行されました。グリッドセルの曇りのパラメータ化が改善されました。 グリッドセルの曇りの割合は、垂直座標のみに依存する臨界相対湿度の経験的プロファイルを使用して診断的に計算された、曇った凝縮水の平均大規模比率に指数関数的に依存すると想定されます。アルベドと表面の放射率に対する雪の影響の別のパラメータ化が実装されました。 大気境界層のパラメータ化、および長波放射のパラメータ化も改善されました。変更が行われた後、季節的な時間スケールでの実用的な予測可能性を評価することを目的とした国際実験SMIP-2 / HFPのプロトコルに従って、NCEP / NCAR再分析データに基づいて遡及的季節予測を計算するために数値実験が実行されました。 これらの実験の結果は、モデルの以前のバージョンの結果と比較されました。予後アンサンブルを計算するための初期データは、6日の00UTCから最初の月の前月の30日の12:00までの期間の12時間シフトの再分析-2NCEP | NCARデータから取得されました。予測。 4か月間の予測が計算され、2〜4か月の平均ACの再現の精度が推定されました。冬の季節予報は、10月末の初期データから始まります。 25年間の季節予報のアンサンブルは、4つの季節のそれぞれについて計算されました。モデルの新しいバージョン(0.225°×0.81°、51レベル)では、熱帯のすべてのフィールドのすべての推定値が大幅に改善されました。 したがって、海面での圧力場の場合、標準偏差は平均で11.6倍減少しています。 850 hPa(T 850)の温度では、同じ誤差が約0.4度(または17%)減少し、降水量では27%減少しました。モデル表面からの蒸発を増加させる地表面の植生を考慮に入れることにより、モデルの新しいバージョンでは熱帯降水量の再現が大幅に改善されたため、モデルの新しいバージョンでは降水量が現れましたほぼ赤道の南アメリカで。 125南極大陸でのT850エラーの顕著な減少は、ISBAパラメータ化の表面に氷が含まれていること、および安定した境界層の記述がわずかに改善されていることに関連しています。 T 850と、程度は少ないがH500の推定値を改善するという目に見える効果は、長波放射の新しいパラメーター化によって与えられました。 12月から2月の期間の予測では、放射線パラメータ化の置き換えによって引き起こされたRMSの減少は0.25でした。 0.4;北半球の温帯低気圧、熱帯、南半球の温帯低気圧の領域では、それぞれ0.35度です。 6月から8月の期間の予測では、改善値は0.9です。 0.4;それぞれ0.15度。 500 hPa(H500)の表面のジオポテンシャルのフィールドの推定値に対する新しいパラメーター化の影響は、主に熱帯地方で明らかになり、RMSDは6月から8月の期間で20.3から11.7 mに、23.8から8月に減少しました。 12月から2月の期間の15.4..。モデル実験のデータから計算されたACの最初の自然直交成分は、再解析のデータから得られた類似の成分に類似しています-2。北大西洋振動の再現における誤差は、大気と海洋の共同モデルで減らすことができます(Tolstykh、Kiktev、Zaripov、2010年)。現在、ロシア連邦の水文気象センターで最大10日間の天気予報を計算するための基本モデルは、有限差分モデルSLAVであり、次のバージョンでは、水平解像度を10kmにする予定です。将来的には、モデルは非静水圧になります(Vilfand、2012)。 第5章へつづく |