|
|
| ミランコヴィッチメニューへ戻る 一般大気循環理論 224p ロシア語 モホフ、A.V。エリセエフ、K.M.。 シャンタリンスキー https://core.ac.uk/download/pdf/197368962.pdf 第1章 第2章 第3章 第4章 第5章 第6章 第7章 参考 第3章 大気のエネルギー 3.1 角運動量バランス. 3.2 水分バランス. 3.3 エネルギーバランス. 3.4 大気の一般循環のエネルギー 大気のエネルギーは、海洋、大気、リソスフェア、雪氷圏、生物圏の5つの相互作用するコンポーネントで構成される気候システム(CS)のエネルギーのコンポーネントです。 COPでは、5つの惑星環流(サイクル)が実行されます。 水分、熱、衝撃、ガス、塩が相互接続されています。作業に続いて、CCにおけるグローバルな熱伝達の形成の特徴を考えてみましょう(Doganovskiy、Malinin、2004)。大気の上限は、地球から太陽までの平均距離が1368 W / m2に等しい短波太陽放射(SR)のフラックスを受け取ります。これは、100%と見なされます。さらに、CCへのすべてのタイプの熱流入は、太陽定数の何分の1かで推定されます(図3.1)。 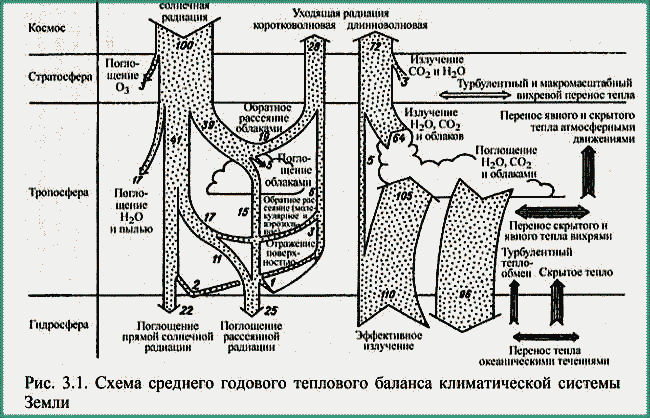 図: 3.1。地球の気候システムの平均年間熱収支のスキーム この図によると、短波放射の28%が宇宙空間に反射されます(雲のため-19%、分子およびエアロゾル散乱-6%、下にある表面から) -3%)。入ってくるSRの一部(25%)は大気に吸収され、3%は成層圏オゾン、17%は水蒸気、5%は雲によって占められています。 残り(47%)は地球の表層に吸収され、ほぼ例外なく、直接および散乱放射の流れの形で世界の大洋に吸収されます(海洋の質量は大気の質量の270倍、熱容量は1000倍です)。 CC自体では、海洋と大気の固有の放射により、長波放射のフラックスが形成されます。 下にある表面から宇宙への長波長放射フラックスは5%、大気への放射フラックスは110%であり、圧倒的な部分(105%)は水蒸気、二酸化炭素、雲、およびさまざまな不純物によって吸収されます。同時に、大気の放射は宇宙(67%)と地表(96%)の両方に発生します。その結果、宇宙空間への全長波放射フラックスは72%であり、地球と大気の境界面では14%であり、上向きです。大気の上限でバランスが観察されます。 つまり、入ってくる放射フラックスと出ていく放射フラックスの合計はゼロです。大気と下にある表面との間の界面で熱平衡を維持するために、熱エネルギーの35%が熱と湿気の乱流の形で下にある表面から大気に伝達される必要があります(8%が占められます)顕熱フラックスによる、および25%-潜熱フラックスによる)..。 3.1 角運動量のバランス 気候システムにおける角運動量の回転のメカニズムを考えてみましょう。地球の軸に対する質量単位の絶対角運動量を計算する式は、次の形式になります(Oort、1988):cos22aMcosua、(3.1)ここで、は地球の角速度です。回転、aは地球の平均半径、φは緯度、uは帯状速度成分(東に正の方向)です。 (3.1)の右辺の最初の項はモーメントと呼ばれ、2番目の項は相対角運動量と呼ばれます。  ここで、ρは密度、tは時間、рは圧力、λは経度、Fλは摩擦力の帯状成分(東に正の方向)です。式(3.2)によると、単位体積あたりの絶対角運動量の変化率は、体積に作用する圧力と摩擦力の合計によってバランスが取られます。単位面積の上の大気の垂直柱上で(3.2)を積分した後、右側は2つの項に分割されます。1つ目は山によって作成された抵抗を表し、2つ目は摩擦、つまりとの相互作用を表します。下にある表面。緯度y1とy2の間に囲まれた帯状リング全体にわたって式(3.2)を積分すると、次の形式になります。  ここで、積分はリング内にある大気の全体積にわたって実行されます。 (3.3)では、山によって作成された抵抗を表す用語Pは、次のように表すことができます。  フォームの摩擦抵抗  (3.4а)、(3.4b)(iWiEPP)-i番目の山の東と西の斜面の圧力差、0-表面の応力。 全導関数を部分導関数で置き換えた式(3.3)は、次の形式を取ります。 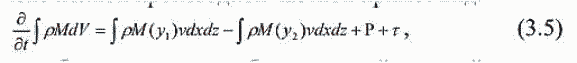 ここで、最初の積分はボリューム全体で行われ、2番目と3番目は緯度y1とy2の縦方向の高さのセクションでそれぞれ行われます。 (3.5)の右辺の第1項と第2項は、北と南の境界を横切る角運動量の交換を表し、最後の2つの項は、山と摩擦によるソースとシンクを表します。また、緯度円を通る総質量流束が小さいため、角運動量交換への主な寄与は、子午線速度成分(北に正の方向)との相関を介した相対角運動量に由来することにも注意してください。 帯状成分u。図では3.2は、大気風の直接測定(avucos)から計算され、年間平均された観測された角運動量バランスを示しています。角運動量は熱帯の地球の表面から伝達され、ハドレーセルで上向きに運ばれ、次に大気の上部85層で極に移動し、中緯度で地球に戻されます。北半球の中緯度では、波が南西から北東に傾いているため、大規模な渦が北への輸送を行っています。南半球では、南へのモーメントの伝達は、南東から北西への波の「傾き」によって形成されます(図3.3)。 図に示す回路では。 3.2では、u風成分とv風成分の間に次の関係が保証されます。北半球では[v * u *]> 0、南半球では[v * u *] <0(角括弧はゾーン平均を示し、アスタリスク-偏差ゾーン平均から)。ああ。オールトは、角運動量の全体的な大気サイクル、赤道から極への角運動量の子午線移動のメカニズムが十分に説明され、理解されているが、地球自体の角運動量の変換についてはほとんど何も知られていないと述べています。 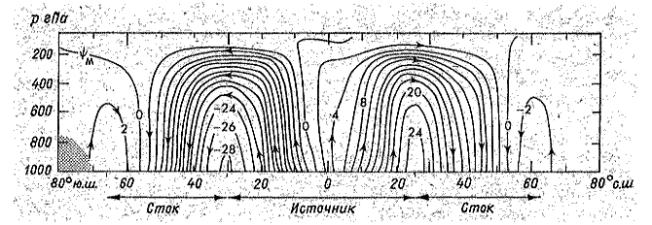 図: 3.2 相対角運動量フラックスのゾーン分布(1018 kg m -2 および30ºN、および中緯度と高緯度での流出。 中緯度から赤道への角運動量の戻りが必要であると想定されます。これは、海洋、固体地球、またはこれらの媒体の両方で発生する可能性があり、角運動量フラックスの方向は次のようになります。大気中のフラックスの方向。推定によると、海洋における角運動量の伝達は大気中よりもはるかに弱いため、角運動量が赤道に伝達される別のメカニズムが検討されています。 大気中の典型的な風速は10m s -1であり、中緯度で直接観測された垂直および円形に平均化された北向きの角運動量[vu]は10 m 2 s-2です。海洋では、通常の流速は高くなく、約0.01〜0.1 ms -1であるため、[vu]の値は0.001 m2 s -2であり、大気の104分の1です。そして、海洋の質量が大気の質量よりもはるかに大きいという事実にもかかわらず、海洋における角運動量の伝達はまだ弱いです。  図: 3.3。 中緯度での準水平渦による西角運動量の極への伝達の主なメカニズムの概略図北半球の流線の優勢な南西-北東斜面および南半球の南東-北西斜面は流れを生成します風成分uとυの相関によって両方の半球の極に。 ああ。オールトは、実際の海が角運動量を帯状にのみ伝達し、子午線方向には伝達しないという事実の結果を考慮することを提案しています。この場合、海洋は、大気と大陸の間の仲介役である伝達リンクとして機能し、特定の緯度帯の大陸に角運動量を与える必要があります。海側から大陸に作用し、大陸の境界に沿ったレベルの上昇または下降によって生成される力があると想定されます-山によって生成される大気中の圧力と非常に似ています(図3.4)。大陸に作用する力は次のように表されます。 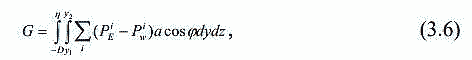 ここで、積分は緯度帯で囲まれた海の体積に対して計算されます。式(3.6)(i wiPEP)は、i番目の大陸または海山の西側と東側の斜面の底部圧力87の差、Dは海の深さ、はジオイドに対するレベルです。総応力への主な寄与は、大陸の端の海面差から来ています。大陸の西と東の境界での海面の差は約50cmです。低緯度では、貿易風が海の東岸の水位を低下させ、大陸に作用する西向きの力を生み出します。中緯度では、西向きの大気輸送の領域で東向きの力が発生します。 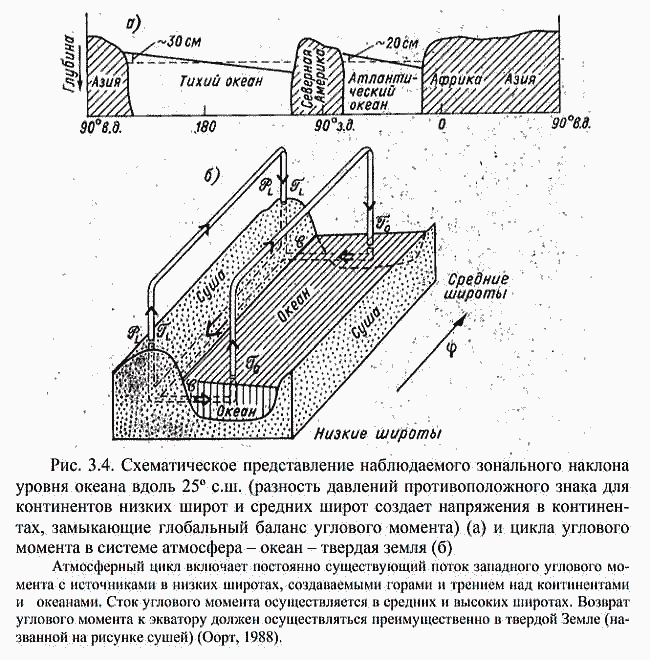 図: 3.4。 25°Nに沿って観測された帯状の海洋レベルの傾きの概略図。 (低緯度と中緯度の大陸の反対の符号の圧力差は、大陸に応力を発生させ、角運動量のグローバルバランスを閉じます)(a)およびシステム大気-海洋-固体地球における角運動量のサイクル( b)大気サイクルには、山と大陸と海の摩擦によって作成された低緯度のソースを伴う、常に存在する西部の角運動量のフラックスが含まれます。角運動量のシンクは、中緯度と高緯度で発生します。赤道への角運動量の戻りは、主に固体地球(図では土地と呼ばれる)で実行する必要があります(Oort、1988)。 大陸に作用する力の定量的評価は、主な役割が海と大陸の間の角運動量の交換によって果たされることを示しました。 A.Khによるとバランスをとるために必要なオルサは、中緯度から低緯度への角運動量のフラックスがほぼ完全に固体地球で形成されています。この流れは、主に大陸の断層に沿って、北半球の中緯度の南東から北西に向いた地殻剪断を通り、南西-南半球の中緯度の断層に沿った北東の断層を通る動きによって実行できます。この図の概念的な力は、大気と海洋の動きを地球の地殻のいくつかの動きと関連付けています。 3.2 水分バランス 大気中の水分の再分配は、地球上の生命を維持するために不可欠であり、気候システム内の物理的物質のバランスを形成します。ラジオサウンディングデータを使用して、子午線および垂直方向の水分移動を計算できます。量vq] [、ここでqは水蒸気の質量分率です。図では3.5は、水循環の大気分岐を示しています。これは、半球の亜熱帯海洋の水分源と、熱帯および中緯度の収束帯内の流出を示しています。この場合、ほとんどすべての水蒸気は対流圏の下層で輸送されます。  図: 3.5 大気中の水分フラックス(1018 kg s-1)の平均帯状分布流線は、亜熱帯および赤道付近(IBCの熱帯収束帯)および中央部に発生源がある大気中の平均年間水分フラックスを特徴づけます。緯度。 大気全体の縦ベルトの水分バランスは、次の形式で記述されます。 ここで、Eは地表からの蒸発速度、Pは降水速度です。式(3.7)によると、緯度帯の含水量の変化率は、南または北の境界を通る水蒸気の流入または流出、および地表での降水量と蒸発量の差によってバランスがとられています。完全なバランス方程式には、水循環の陸域部分からの代償的な流出がさらに含まれます。ここで、流れは赤道と中緯度から亜熱帯に向けられます。縦ベルトの陸域の液体水分のバランス(蓄積率を無視)は、次のように記述されます。 ここで、右側の積分は海洋セクションで計算されます。Rは河川と地下流出による水分の再分布率、ρоは海水の密度です。左側がわかっている場合(蒸発と降水の差)、子午線の水流は式(3.8)を使用して計算できます。研究(Doganovsky、Malinin、2004)では、子午線水分移動のさまざまなモードの分布の分析(図3.6)が示され、それに応じて、20°Nからのゾーンで行われます。 20ºSまで平均流量が優勢です。冬は南向き、夏は北向きです。北半球の定常的な水分の流れは、南半球よりも顕著です。夏には亜熱帯地域で、冬には50〜60°Nの地域で最大に達します。これはアイスランドとアリューシャンの低気圧の発達に関連しています。不安定な水分の流れは、一年のすべての季節に極に向けられます。サイクロン活動が最も発達している温帯および高緯度では、非定常流が他の子午線流と比較して支配的です。 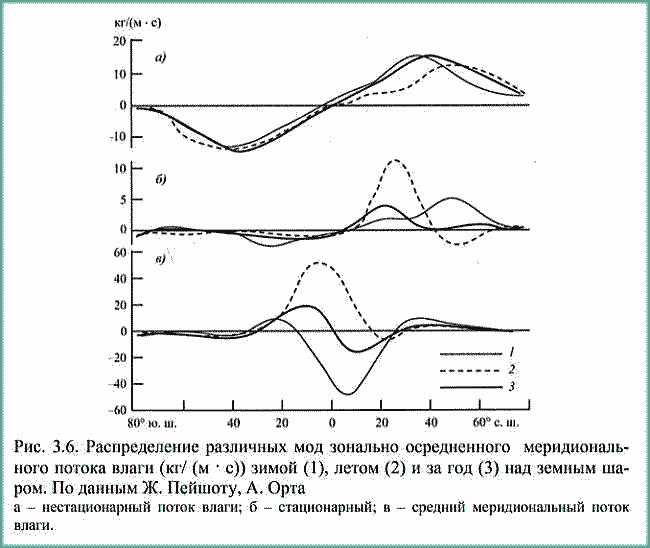 図: 3.6。 帯状に平均化された子午面水分フラックスのさまざまなモードの分布(kg /(m J.PeixhotとA.Ortaによると、-不安定な水分の流れ。 b-静止; c-平均子午線水分流量。 3.3 エネルギーバランス A.Kh. Oortは、ラジオサウンディングデータから大気中のエネルギーフラックス[v(ρe+ P)]を計算しました。ここで、eは総エネルギー(ポテンシャル、内部、運動エネルギー、潜在エネルギーの合計)、Pは大気圧です。 図では 3.7は、大気中のエネルギーフラックスのゾーン平均セクションを示しています。 低緯度では、エネルギーは中部子午面循環によって伝達され、中緯度では、大規模な渦によって伝達されます。 緯度リングと大気の厚さ全体にわたって平均化された、大気中のエネルギーバランス方程式は次のように記述されます。 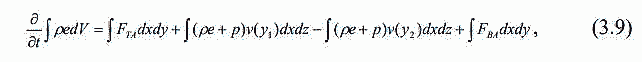 ここで、FTAは大気の上部境界での下降放射フラックスであり、FBAはその下部境界での下降エネルギーフラックスです。 式(3.9)は、緯度帯のエネルギー量の変化率が、大気の上下の境界、側壁、および側壁の圧力の作用によるエネルギーの流入と流出によってバランスが取れていることを示しています。 。 平均的な年間条件については、(3.9)の左側の項は無視できます。 海の厚さ全体を含む、地球の表面の緯度帯のエネルギーバランスは、次の形をしています。 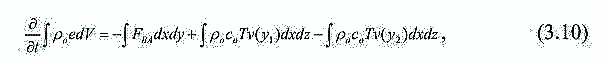 ここで、右側の移流の積分は海洋セクションで計算されます。ωは海水の熱容量です。 式(3.10)では、エネルギーの変化率は、海面を横切るエネルギーの流れと、電流によって生成される水平方向の熱交換によってバランスがとられています。 平均的な年間条件では、(3.10)の左側は無視できます。 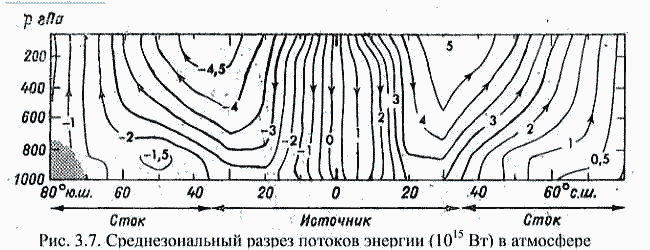 図: 3.7。 大気中のエネルギーフラックス(1015 W)のゾーン平均セクション 式(3.9)と(3.10)を使用してバランス方程式の残余項として計算された海洋のエネルギー伝達を図1に示します。 3.8。 この図の曲線は、放射、大気エネルギーの貯蔵と輸送、および海洋貯蔵に関する完全なデータから計算されており、バランス方程式の残りの部分として定義されています。 ああ。 Oortは、一般的な信念に反して、海洋の熱流は強い季節変動を経験することを強調しています。 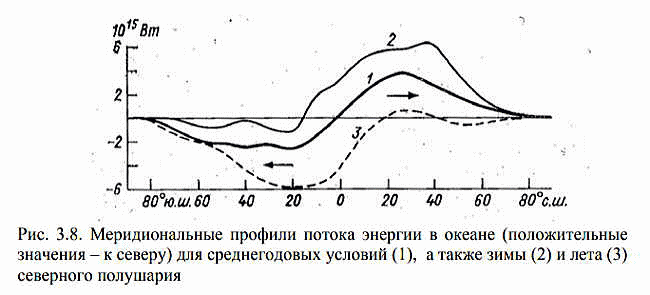 図: 3.8。 北半球の冬(2)と夏(3)だけでなく、平均的な年間条件(1)に対する海洋のエネルギーフラックスの子午線プロファイル(正の値-北へ) したがって、Oort(1988)は、熱帯の中緯度からの角運動量の必要な戻りが海洋ではなく大陸プレートで発生するという証拠を提供しています。海と陸の亜熱帯からの水蒸気の流れの存在が確認されました。大きな季節変動を特徴とする極への海洋における強い熱流束の存在、および冬半球の赤道を横切る強力な熱流束の存在についての以前の仮説の妥当性が確認された。 3.4。大気の一般循環のエネルギー OCAの主なエネルギー源は太陽熱であり、平均速度約1356 W / m2で地球に流入します。反射された放射線(平均0.28の惑星アルベド)を考慮に入れると、同化された放射線は、1日あたり地球の表面積の単位あたり平均244 W / m2です。大気の内部エネルギーは8.6・1023Jと推定され、ポテンシャルは3.6・1023Jです。言及されたタイプのエネルギーの合計は、総エネルギーまたは不安定エネルギーと呼ばれます(Monin、1982)。大気の利用可能な位置エネルギー(APE)は、全位置エネルギーと安定した静水圧平衡にあるエネルギーとの差として定義されます。これは、運動エネルギーに変換できる全位置エネルギーの一部を表しています(Lorentz、1970)。 DPE値は、1955年にローレンツによって得られた式によって概算できます。  ここで、Cpは一定圧力での空気の比熱容量、аは乾燥断熱温度勾配、2Тは等圧表面の温度分散の加重値、は垂直温度勾配、上のダッシュは平均化を意味します等圧面上。 Oort(1964)によると、DPEは5.5・106 J / m 2であり、大気の運動エネルギーは1.5・106 J / m2です。 Borisenkov(1960)によると、北半球では夏に1.9×1020 J、冬に4×1020 J、南半球では夏に3.9×1020、冬に7.1×1020Jです。 (Monin、1982)によると、1.25×1014 kWの電力で地球に吸収された太陽放射のエネルギーは、大気と海と大陸の上層の直接加熱に2/3、そして31-に費やされます。地表からの水分の蒸発について。 同化された放射線のごく一部だけが大気運動の運動エネルギーの生成に費やされます(運動エネルギーの生成速度は4 W / m 2のオーダー、つまり同化された放射線のパワーのわずか1.6%です) )。したがって、大気の運動エネルギーは全体のごく一部(約6%)であり、1週間以内に摩擦による熱への放散が発生する可能性があります。 Oortの推定によると、大気の主なエネルギーサイクルは、2A3.2/ Bt t / mの速度での熱流入による、利用可能な位置エネルギーA = 5.5 106 J / m2の生成で構成されます。運動エネルギーK = 1.5×106J / m 2への同じ速度と、後者の熱への散逸はすべて同じ速度23.2/ BtK t / mです(Monin、1982)。エネルギーを平均帯状エネルギー(M)とゆらぎエネルギー(E)の2つの成分に分割すると、エネルギーサイクルを図の形で表すことができます(図3.9)。 図では3.9次の指定が使用されます。A-利用可能な位置エネルギー。 K-運動エネルギー; Gは生成エネルギー、Dは散逸エネルギーです。矢印は、エネルギー変換の方向を示しています。図からわかるように。 3.9、平均帯状循環AMのAPのエネルギーは変動AEのエネルギーに変換され、CMの帯状運動の運動エネルギーはより小さなスケールKEの運動の運動エネルギーに変換されます。 DPE 94の生成速度と、平均運動および渦運動のFEの散逸速度が示されています。あるタイプから別のタイプへのエネルギーの遷移は、対応する大気の動きの存在下で発生することに注意してください。 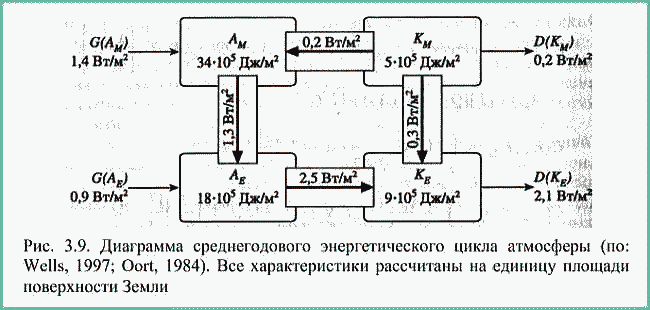 図: 3.9。 大気の平均年間エネルギーサイクルの図(作成者: ウェルズ、1997; Oort、1984)。 すべての特性は、地球の表面の単位面積ごとに計算されます この本(Kalinin、2001)は、地球の大気中の主な種類のエネルギー(ポテンシャル、内部、運動)のバランス方程式を、エネルギー変換の詳細な物理的解釈とともに積分形式で示しています。ここでは、ローレンツ(1970)によって提案されたエネルギー変換のスキームに言及することに限定します。 これによれば、エネルギーは4つのタイプ(ゾーン利用可能ポテンシャル、渦利用可能ポテンシャル、および渦運動)に分割され、ラジオゾンデ測定が電力の推定に使用されます。渦の移動と中間子午線の動きによる各タイプの遷移の変化。象徴的に、帯状成分と渦成分の利用可能なポテンシャルと運動エネルギーのバランスに関する連立方程式は、通常、次の形式で記述されます。 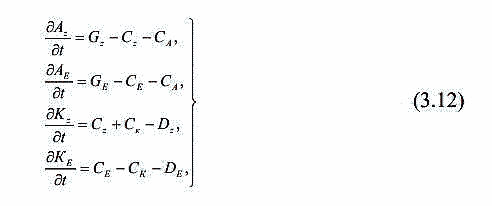 ここで、АzとАЕ-帯状および渦状のDPE。 Кz、КЕ-帯状および渦状FE; Gz、GE-帯状および渦状DPEの生成率。 Dz、DE-帯状および渦状FEの散逸率。 Сz、СE-АzからKzへの遷移速度、およびАЕからКЕへの遷移速度。 CA、CK-АzからАЕへの遷移速度とКЕからKzへの遷移速度。利用可能な位置エネルギーは、準帯状大気流の流体力学的不安定性の条件下で大気中に発生するシノプティック渦の発達のためのエネルギー源であることが知られています。 (Shakina、1985)によると、さまざまなタイプの流体力学的不安定性の中で、大規模な乱気流形成のプロセスで最も重要な役割は傾圧不安定性によって果たされます。 コリオリの力場における緯度方向の温度勾配(および風速の垂直方向の勾配)を伴う大気流の不安定性。傾圧不安定性(コリオリの力の場での横方向のウィンドシアによる大気流の不安定性)の場合、シノプティック渦のエネルギー源は主流の運動エネルギーです。オン。 Kalinin(1999)は、温帯緯度のサイクロン形成の進化のさまざまな段階で、総渦運動エネルギーと利用可能な位置エネルギー貯蔵量の信頼できる定量的推定値を取得しました。 (Kislov、2001)では、気候システム大気のエネルギー収支-海洋の活性層が考慮され、秩序化された渦の移動による緯度間のエネルギー移動の強度が推定されます。北半球と南半球の海洋における熱伝達は、大西洋、太平洋、インド洋の水のダイナミクスの特性によって決定されることがわかりました。 1992年から2001年の期間に対流圏の利用可能なポテンシャルと運動エネルギーを監視した結果を考えてみましょう。ご存知のように、エネルギー変換は、大気循環(GCA)の主な特徴、惑星と地域の気候、および気象プロセスの形成において重要な役割を果たします。 この研究(Guryanov、Perevedentsev、2003)は、20世紀の終わりに地球の気温が最大に上昇した期間中のローレンツエネルギーサイクルのいくつかの特性の計算結果を示しています。帯状および渦の利用可能な位置エネルギー(ZDPEおよびVDPE)、帯状および渦運動エネルギー(ZKEおよびVCE)..。 エネルギーの種類の計算は、よく知られている式(Oort、1964)に従って行われました。得られた値は単位面積を基準とし、105 J / m2の寸法を持ちますが、簡潔にするためにさらに省略されています。初期データは、英国大気データセンターの気温、帯状および子午線風速成分に関する毎日のデータでした(UKMOアーカイブ-UARS同化データ)。 データは、1992年から2001年の期間に、1000、681、464、316、215、146、および100 hPaの等圧面上の球全体にわたって、2.5ºx3.75ºの通常の緯度-縦方向グリッドのノードに表示されます。計算は、北半球と南半球(SPとSP)および球全体に対して実行されました。経年変動を評価するために、上記のタイプのエネルギー(RMS)の標準偏差の値が計算されました。 10年間の各月について得られた結果を分析した結果、以下の規則性が明らかになりました(表3.1および3.2に示されている値は全期間の平均です)。 運動エネルギーと利用可能な位置エネルギーの予備の得られた値は、(Oort and Peixoto、1974)で与えられた値とよく一致しています。冬の北半球の渦DPEの値はやや過小評価されているように見えます。おそらくこれは、下にある表面の影響による温度コントラストが上部対流圏よりもはるかに大きい850hPa表面を計算が考慮していなかったという事実によるものです。 表に示されている、考慮されているすべての種類のエネルギー。 3.1と3.2は、明確に定義された年間変動があり、各半球の冬の期間に最大値、夏に最小値があります。球体では、北半球と南半球の年周期が逆位相であるため、年周期が平滑化されます。 SPでは、ZDPEの値はSPの対応する値よりも約10単位高くなっています。 SPの複数年の平均値の年間コース(表3.1)では、最大値は1月57.3に、最小値は7月14.9に観察されます。 年間変動の振幅(A)は平均42.4です。 SP(表3.2)では、最大値は8月-64.2に、最小値は1月-34.7に観測され、振幅は29.5です。したがって、SPでは、年間コースはSPよりも目立たなくなります。合弁事業におけるZDPEの平均年間価値は37.2(1999)から39.5(1993)まで変動し、平均長期価値は38.7です。 SPの97-48.5(1999)から51.3(1997)まで、長期平均は50.0。全体として、45.3(1999)から2001年の47.9まで(平均長期値46.8)。したがって、1999年には、ZDPEのグローバル最小値が記録されています。 表3.1 層1000-100の北半球の大気のエネルギー貯蔵 1992〜 2001年のhPa、105 J / m 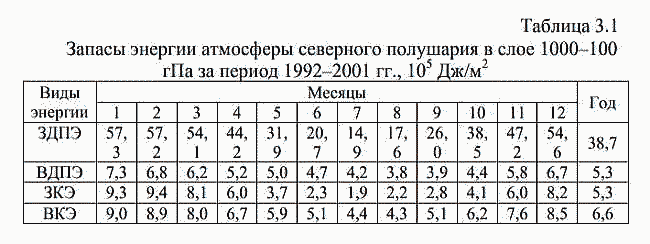 表3.2 1000〜100層の南半球大気のエネルギー貯蔵量 1992〜 2001年のhPa、105 J / m 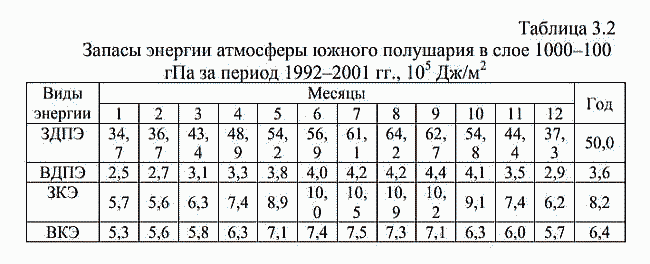 SPのRMSは、7月の0.84から2月の2.27まで変化します(平均年間値の場合は0.66)。 SPで-12月の0.99から8月の3.24まで(平均年間値は1.06)。球体全体では、1.12(3月)から1.94(10月)までで、年間平均は0.80です。したがって、rms偏差はSPで大きく異なります。渦DETは、帯状DETよりも大きさが大幅に劣っています。年間のSPでは、8月の3.8から1月の7.3に変化し、年次振幅は3.5、平均年次値は5.3です。 SPでは-1月の2.5から9月の4.4まで、年間振幅は1.9、平均年間値は3.6です。 SPでは(ZDPEとは対照的に)、渦DPEは北半球よりも予備力が劣っています。全体として、RDPEの領域では、8月の3.9から1月の4.9まで変動し、長期平均値は4.5です。 98合弁事業では、10年間の最小VDPEは5.1(1998)であり、最大は5.7(2001)でした。 SPではこれらの値はそれぞれ3.3(1998)と4.2(2001)であり、球体では-4.2(1998)と5.0(2001)でした。 その結果、検討中の期間の極端な年のSPとSPに一致があります。 1998年には記録的なレベルの地球温暖化があったことに注意してください。渦DPEの経年変動、および帯状変動は、SPでは2月(0.46)、SPでは8月(0.53)に最高値に達します。運動エネルギーの時間経過を考えてみましょう。南半球(8.2)の帯状CE(ZDPEと同様)が北半球(5.3)のZKEの埋蔵量を超えていることは注目に値します。 さらに、逆に、北半球での年周期の振幅(7.5)は、南半球での振幅(5.3)よりも大きくなっています。検討中の期間中、SPのSEEの最小値(4.9)は1999年に観察され、最大値(5.5)は1992年に観察されました。SPでは、SEEの最小値(7.3)が1992年に記録されました。最大(8、3)-1997年。SPの最大年々変動は1月(0.79)に発生し、SP- 9月(0.55)に発生します。 IQEを分析するとき、北半球と南半球でこのタイプのエネルギーの埋蔵量がほぼ同じであるという事実に注意が向けられます(年平均)。ただし、SPの年間サイクルの振幅(4.7)は、SPの類似値(2.2)の2倍です。 SPのIQEの経年変動は、12月(0.50)に最大になり、SP- 8月(0.70)に最大になります。 4種類すべてのエネルギーの経年変動を考慮する場合、1つの興味深い事実に注意する必要があります。 1998年、北半球の寒冷期(特に2月)には、10年間で帯状エネルギーの絶対最大値(SPでは2月に62.0ZDPEと11.3ZKE)があり、渦エネルギーは絶対最小値でした。フォーム(合弁事業の2月の6.1VDPEおよび8.2VKE)。 この期間の南半球では、帯状の運動エネルギーについてのみ異常に高い値が観察されました。さらに、この異常は、1997年7月から1998年6月までのほぼ1年間続いた。非常に激しいエルニーニョ現象が観測されたのは今年だったという点で際立っています。このように、実施された研究は、大気のエネルギーの観点からOCAの大規模な特徴を研究することが賢明であることを示しています。 第4章につづく |